In dynamical systems, a vector represents quantities with magnitude and direction like position, velocity, acceleration, and angular velocity.

Under different other contexts, vectors can mean a different thing.

For example:

1. A vector often refers to an array containing numerical values in software engineering.

2. In linear algebra, a vector can contain symbolic variables that are grouped intentionally for mathematical manipulation.

Vector representation

A vector quantity can be represented graphically or symbolically.

Graphically, we draw it as an arrow.

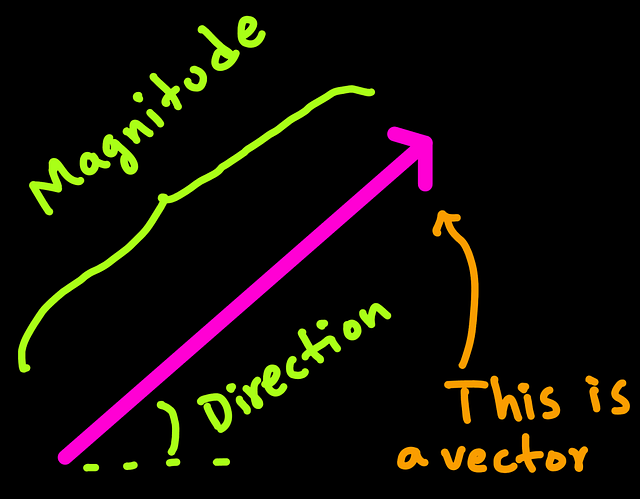
Symbolically, we write it as a bold letter, e.g.

How do we use vectors?

Let’s see how we use vectors graphically and symbolically in the following crane system. Our objective is to use vectors to determine the position of the crane’s payload.

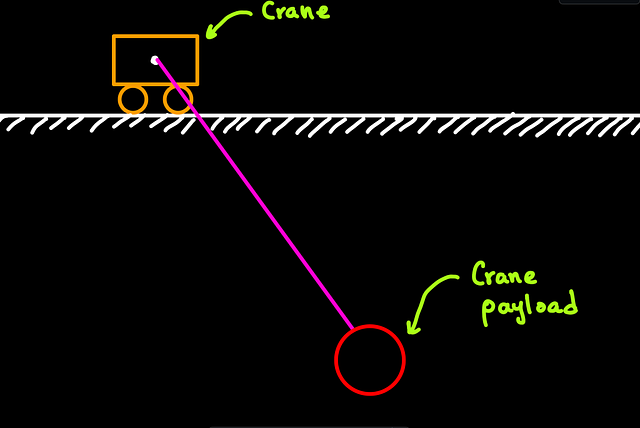
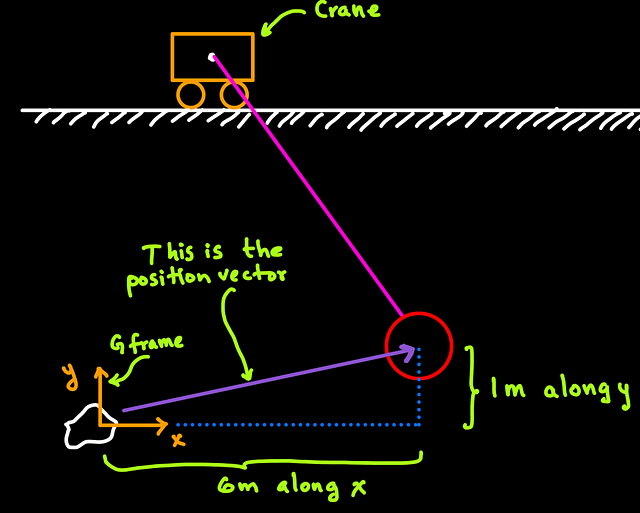
First, we need to establish our reference frame. That is, we are trying to establish the payload’s position, but, with respect to where? I will draw a fixed object at the bottom-left of this diagram, which will be our reference frame. Good!

Next, we need a coordinate system. The coordinate system will allow us to measure quantities. In this case, it will let us measure distances for the position of the crane’s payload. The coordinate system is indicated with directions and needs to be attached to the reference frame as follows:

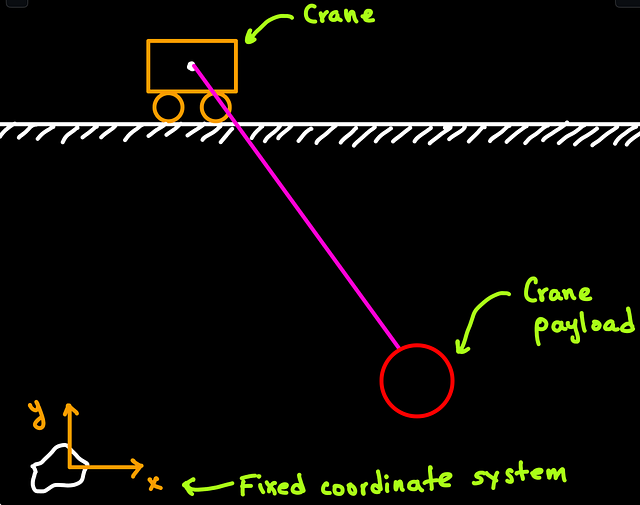
Now, we are ready to use this coordinate system to denote where the payload is. Let’s draw the position vector of the payload with respect to our reference frame and measure the position using the coordinate system.

The symbolic (or mathematical) representation of the vector can be written as

This mathematical notation means that the vector Gp is constructed by adding the vector of 6 units along x and 1 unit along y. The hat over x and y is to make clear that those are vectors only used to specify directions, not quantities.

The left-superscript G means that the vector is written with respect to the coordinate system G.

If we are using only one coordinate system, we could omit the frame name:

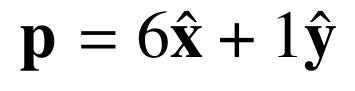
One decides in what coordinate system the vectors in question are represented. For this reason, specifying the coordinate system of a vector is crucial when solving an engineering problem.

Confusing where a vector is being represented is often cause of many system bugs.

Same vector, different representation?

Now, it becomes very interesting because the same vector quantity can be represented in different coordinate systems. For example, imagine installing a velocity sensor on the crane’s payload. Assume that the sensor is attached to the orientation shown in this figure.

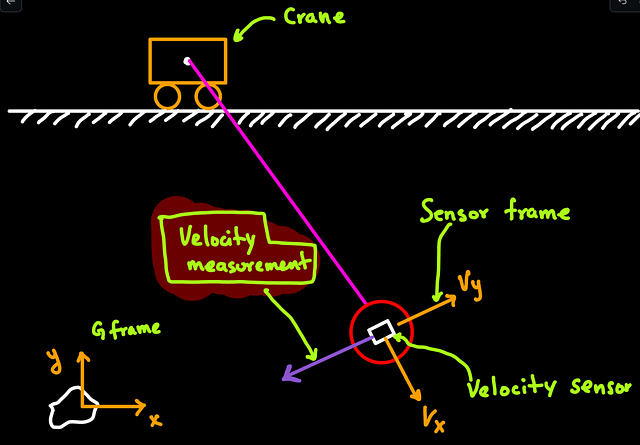
In this scenario, whenever the sensor reads the payload’s velocity, it will report velocity values according to this sensor orientation.

While the sensor may be reporting only velocity values along, e.g., its y-direction (as shown in the figure above), note that we could still describe (measure) that velocity vector using the frame from the bottom-left. The following figure shows that the exact Velocity measurement has components in x and y if we use reference G.

This means that THE SAME vector can be described from DIFFERENT frames.

In particular to this example:

The inertial velocity of the payload is the same regardless of the frame choice. However, the velocity representation is different depending on what frame we use.

Representing vectors in different frames and combining different representations is very powerful when modeling physical systems. This is especially true when dealing with multi-body and multi-sensor systems, such as robotics, aerospace, and modern autonomous car systems.

Visit my other articles and YouTube channel for more!

Thank you!!!