A coordinate system is introduced when we want to measure motion. By measuring motion, we mean obtaining specific numbers that quantify motion or changes. The most common example can be a two-dimensional coordinate system like this:

Here, the x-y coordinate system provides a way to measure motion along the x-direction and the y-direction. With this coordinate system in place, we can talk about, for example, meters along x and meters along y, or velocity along x and velocity along y.

We must note that a coordinate system is overlaid on a reference frame. A reference frame is a rigid body (physical or not) to which the coordinate system will be attached. If we see it this way, we could attach a coordinate system to a rigid body in infinitely different ways, as illustrated in the following figure:

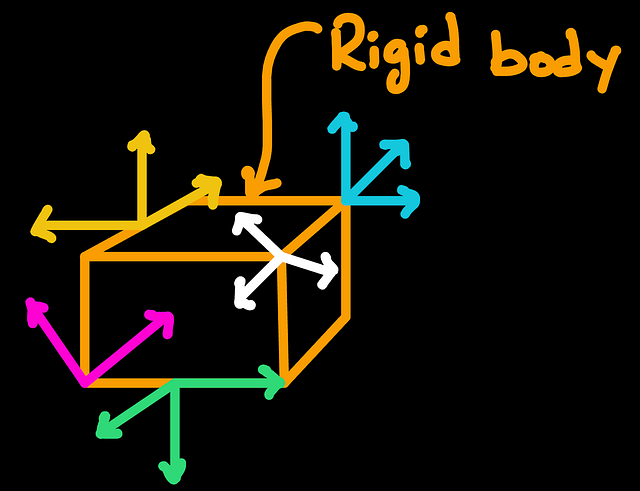
A rigid body can be moving, and the coordinate system can move along with it!

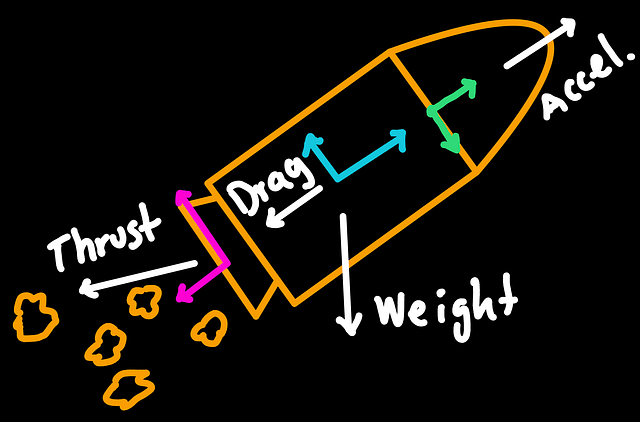
An aerospace engineer can attach different coordinate systems to a rocket. The location and orientation of the coordinate systems attached to the rocket are set according to what it is more convenient to measure quantities like thrust, rocket weight, acceleration, and aerodynamic drag.

How do we establish a coordinate system?

In practice, we use vectors to define a coordinate system. However, there is no restriction on what objects are used for a coordinate system because the general definition states that:

A coordinate system is a group of objects that allow measurement.

For most applications in 3D space, this group of objects will be a set of three orthogonal unit vectors that are defined following the right-hand rule.

Let’s break down this phrase.

Vectors . These vectors indicate the directions along which we measure the motion. Think of East and North directions: you may say 100 m along East, 200 meters along North.

Unit. This refers to the length of the vectors used. A unit vector is a vector with length equal to 1 unit. We could use any length, but that may add unnecessary complexity.

Actually, there is no restriction on the size of these vectors, but unit vectors are convenient.

Orthogonal: This means that the vectors being used are 90 degrees apart from each other. We could use vectors that are not 90 degrees apart, but that can add unnecessary complexity.

It is common to find the word orthonormal as well. That is just to say orthogonal and unit in the same word.

Right-hand rule. Without getting into too much trouble, we will say that this is the rule that help us label the axis.

To label our axis we pick the labels, for example the labels (axis1,axis2,axis3) or (X,Y,Z) or (a1,a2,a3) or (i,j,k).

Suppose that we picked (X,Y,Z). We will do the following to name our axis:

Step 1. Draw a coordinate system. Set the directions in an orthonormal way.

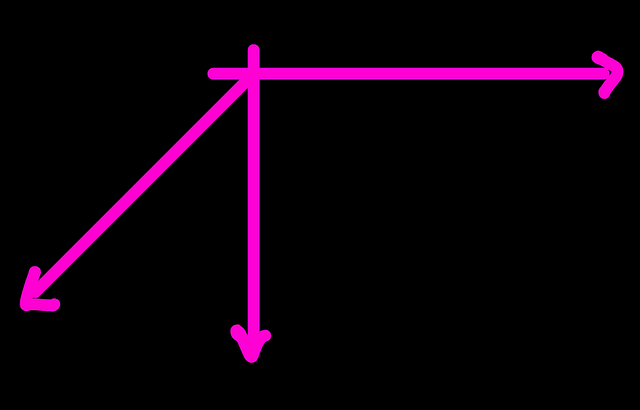
Step 2. We name any of the axis with the first label. X in this case.

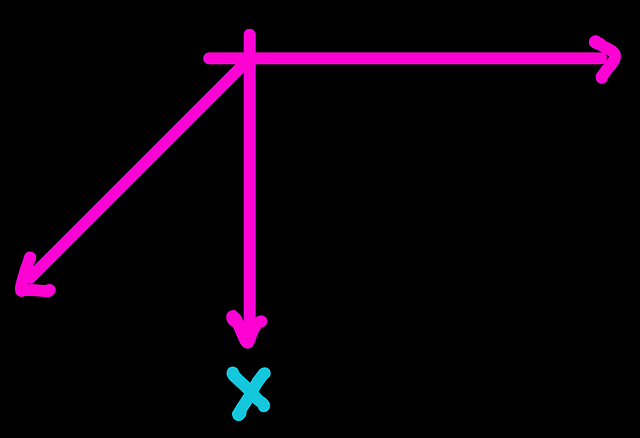
Step 3. We move to the next axis by going 90 deg in a counter-clockwise direction. The axis that we reached will be named with the next label. Y in this case.

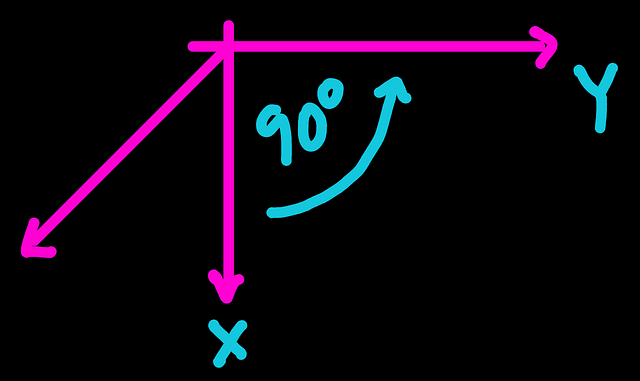
Step 4. Again, we move in a counter-clockwise direction by 90 deg, and the axis reached is named with the last label. Z in this case

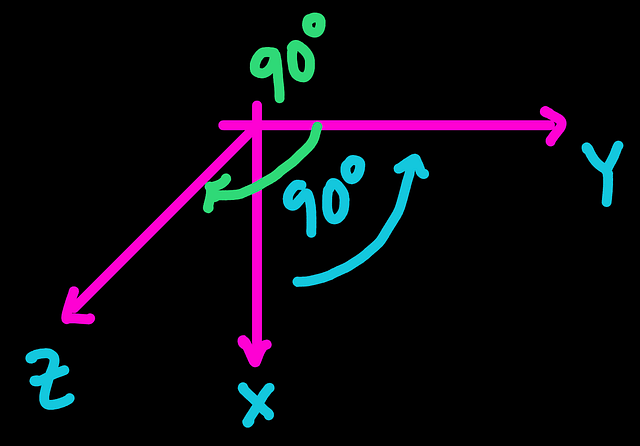
To know which the counter-clockwise direction is, imagine that you are observing the coordinate system from the axis that is not participating in the labeling.

Imagine yourself like this:

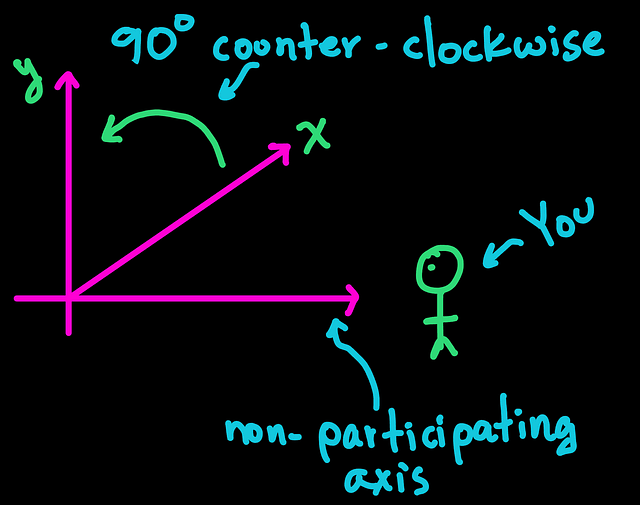
If by going 90 deg in counter-clock direction no axis is reached, the coordinate system does not follow the right-hand rule. In this case, we simply redraw our coordinate system to agree with this counter-clockwise scheme.

We do not necessarily need to draw the origin

Often, one sees the coordinate frame with three vectors meeting at a point called the origin. Like this,

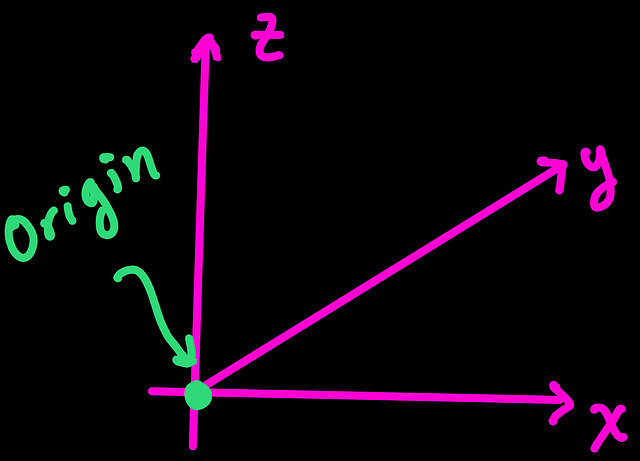
However, this is just for illustrative convenience and we do NOT necessarily need to draw the vectors meeting at the origin.

What is essential to the coordinate system is the direction of the vectors.

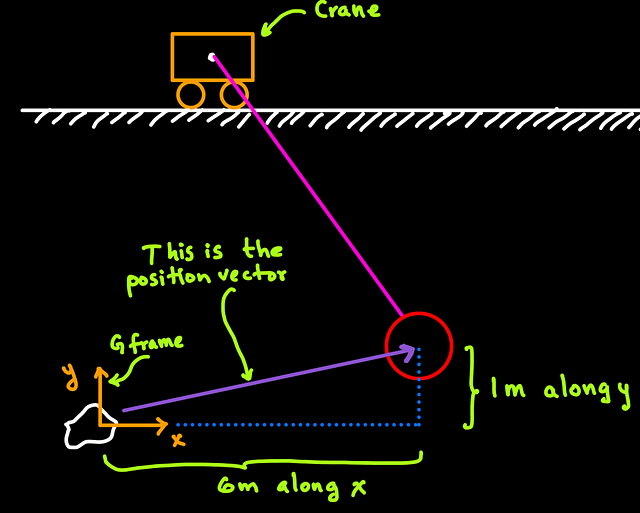
Defining the coordinate system like the following is valid.

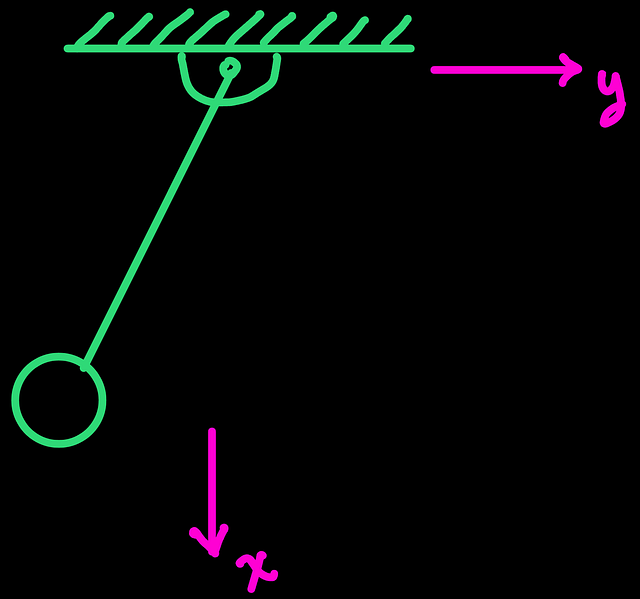
It is valid because we can still measure motion along these (x and y) directions, and if needed, we are able to locate the origin of the coordinate system. Sometimes not joining the axes at the origin can be convenient to improve the clarity of the drawing.